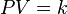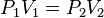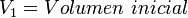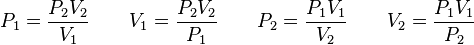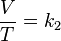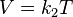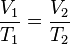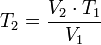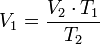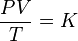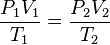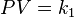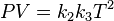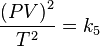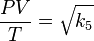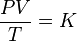QUIMICA 001

GAS IDEAL

Un gas ideal es un gas teórico compuesto de un conjunto de partículas puntuales con desplazamiento aleatorio que no interactúan entre sí. El concepto de gas ideal es útil porque el mismo se comporta según la ley de los gases ideales, una ecuación de estado simplificada, y que puede ser analizada mediante la mecánica estadística.

Las principales leyes que rigen el estado gaseoso son:
a- Ley de Boyle - Mariotte
b- Ley de Jacques Charles I y II
c- Ley de Gay Lussac
d- Ley Combinada - Ecuacion general
e- Ley de Dalton

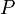$P\!$ = Presión del gas
$V\!$ = Volumen del gas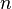
$n\!$ = Número de moles de gas
$R\!$ = Constante universal de los gases ideales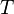
$T\!$ = Temperatura del gas
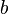$a\!$ y $b\!$ son constantes determinadas por la naturaleza del gas con el fin de que haya la mayor congruencia posible entre la ecuación de los gases reales y el comportamiento observado experimentalmente.

LEY DE BOYLE - MARIOTTE

La Ley de Boyle-Mariotte, o Ley de Boyle, formulada independientemente por el físico y químico irlandés Robert Boyle(1662) y el físico y botánico francés Edme Mariotte (1676), es una de las leyes de los gases que relaciona el volumen y lapresión de una cierta cantidad de gas mantenida a temperaturaconstante. La ley dice que:

La presión ejercida por una fuerza física es inversamente proporcional al volumen de una masa gaseosa, siempre y cuando su temperatura se mantenga constante.

o en términos más sencillos:

A temperatura constante, el volumen de una masa fija de gas es inversamente proporcional a la presión que este ejerce.

Matemáticamente se puede expresar así:

$PV=k\,$

donde

k\,

es constante si la temperatura y la masa del gas permanecen constantes.

Cuando aumenta la presión, el volumen baja, mientras que si la presión disminuye el volumen aumenta. No es necesario conocer el valor exacto de la constante

k\,

para poder hacer uso de la ley: si consideramos las dos situaciones de la figura, manteniendo constante la cantidad de gas y la temperatura, deberá cumplirse la relación:

$P_1V_1=P_2V_2\,$

donde:

$P_1 = Presi\acute{o}n \ inicial \,$
$P_2 = Presi\acute{o}n \ final\,$
$V_1 = Volumen \ inicial\,$
$V_2 = Volumen \ final\,$

Además, si se despeja cualquier incógnita se obtiene lo siguiente:

$P_1=\frac{P_2V_2}{V_1} \qquad V_1=\frac{P_2V_2}{P_1} \qquad P_2=\frac{P_1V_1}{V_2} \qquad V_2=\frac{P_1V_1}{P_2}\,$

Esta ley es una simplificación de la ley de los gases ideales o perfectos particularizada para procesos isotérmicos de una cierta masa de gas constante.

Junto con la ley de Charles, la ley de Gay-Lussac, la ley de Avogadro y la ley de Graham, la ley de Boyle forma las leyes de los gases, que describen la conducta de un gas ideal. Las tres primeras leyes pueden ser generalizadas en la ecuación universal de los gases.

LEY DE CHARLES I

La Ley de Charles y Gay-Lussac, o simplemente Ley de Charles, es una de las leyes de los gases. Relaciona el volumen y la temperatura de una cierta cantidad de gas ideal, mantenida a una presión constante, mediante una constante de proporcionalidad directa.

La ley fue publicada primero por Gay Lussac en 1803, pero hacía referencia al trabajo no publicado de Jacques Charles, de alrededor de 1787, lo que condujo a que la ley sea usualmente atribuida a Charles. La relación había sido anticipada anteriormente en los trabajos de Guillaume Amontons en 1702.

Por otro lado, Gay-Lussac relacionó la presión y la temperatura como magnitudes directamente proporcionales en la llamada "La segunda ley de Gay-Lussac".

Volumen sobre temperatura: Constante (K -en referencia a si mismo)

$\frac{V}{T} = k_2$

o también:

$V = k_2T \qquad$

donde:

V es el volumen.
T es la temperatura absoluta (es decir, medida en Kelvin).
k₂ es la constante de proporcionalidad.

Además puede expresarse como:

$\frac {V_1}{T_1} = \frac {V_2}{T_2}$

donde:

V_1\,

= Volumen inicial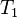

T_1\,

= Temperatura inicial

V_2\,

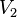= Volumen final

T_2\,

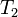= Temperatura final

Despejando T₁ se obtiene:

$T_1 =\frac {V_1 \cdot T_2}{V_2}$

Despejando T₂ se obtiene:

$T_2 =\frac {V_2 \cdot T_1}{V_1}$

Despejando V₁ es igual a:

$V_1 =\frac {V_2 \cdot T_1}{T_2}$

Despejando V₂ se obtiene:

$V_2 =\frac {V_1 \cdot T_2}{T_1}$

Un buen experimento para demostrar esta ley es el de calentar una lata con un poco de agua, al hervir el agua se sumerge en agua fría y su volumen cambia.

LEY DE GAY LUSSAC

La ley de Gay-Lussac establece que la presión de un volumen fijo de un gas, es directamente proporcional a su temperatura.

Si el volumen de una cierta cantidad de gas a presión moderada se mantiene constante, el cociente entre presión y temperatura (kelvin) permanece constante:

$\frac{P}{T} =k_3$

o también:

P = k_3T \qquad

donde:

P es la presión
T es la temperatura absoluta (es decir, medida en kelvin)
k₃ una constante de proporcionalidad

Esta ley fue enunciada en 1802 por el físico y químico francés Louis Joseph Gay-Lussac.

Para una cierta cantidad de gas, al aumentar la temperatura, las moléculas del gas se mueven más rápidamente y por lo tanto aumenta el número de choques contra las paredes por unidad de tiempo, es decir, aumenta la presión ya que el recipiente es de paredes fijas y su volumen no puede cambiar. Gay-Lussac descubrió que, en cualquier momento del proceso, el cociente entre la presión y la temperatura absoluta tenía un valor constante.

Supongamos que tenemos un gas que se encuentra a una presión

\scriptstyle P_1

y a una temperatura

\scriptstyle T_1

al comienzo del experimento. Si variamos la temperatura hasta un nuevo valor

\scriptstyle T_2

, entonces la presión cambiará a

\scriptstyle P_2

, y se cumplirá:

$\frac{P_1}{T_1} = \frac{P_2}{T_2}$

donde:

P_1\,

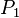= Presión inicial

T_1\,

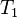= Temperatura inicial

P_2\,

= Presión final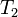

T_2\,

= Temperatura final

Que es otra manera de expresar la ley de Gay-Lussac.

Esta ley, al igual que la ley de Charles, está expresada en función de la temperatura absoluta. Es decir, las temperaturas han de expresarse en kelvin.

LEY COMBINADA

Esta ley establece como enunciado:

"El volumen ocupado por una masa gaseosa, es inversamente proporcional a las presiones y directamente proporcional a las temperaturas absolutas que soportan"

quimicaenaccion.wikispaces.com

Observa la siguiente imagen a través de la cual se comprueba el enunciado de la presente ley:

De acuerdo con el enunciado, se puede establecer la siguiente expresión matemática:

V1 . P1 = V2 . P2

T1 T2

En donde:

V= Volumen

P= Presión

T= Temperatura

Observa en los siguientes ejemplos la aplicación de dicha expresión:

1. Una masa gaseosa ocupa u volumen de 2,5 litros a 12 °C y 2 atm de presión. ¿Cuál es el volumen del gas si la temperatura aumenta a 38°C y la presión se incrementa hasta 2,5 atm?

· Primer paso: identificar los datos que brinda el enunciado.

V1= 2,5 L

T1= 12 °C

P1= 2 atm

T2= 38 °C

P2= 2,5 atm

· Segundo paso: Conocer la incognita.

V2= ?

· Tercer paso: Despejar V2 de la expresión V1 . P1 = V2 . P2 , quedando así:

T1 T2

V2= V1 . P1 . T2

T1 . P2

· Cuarto paso: Transformar las unidades de temperatura (°C) a Kelvin.

T1: K= °C + 273 T2: K= °C + 273

K= 12 + 273= 285 K K= 38 + 273= 311 K

· Quinto Paso: Sustituir los datos en la expresión y efectuar los calculos matemáticos.

V2= 2,5 L . 2 atm . 311 K

285 K . 2,5 atm

Se cancelan las unidades de presión y temperatura (atm y K), se obtiene el resultado.

V2= 2,18 L

ECUACIÓN GENERAL

La ley combinada de los gases o ley general de los gases es una ley de los gases que combina la ley de Boyle, laley de Charles y la ley de Gay-Lussac. Estas leyes matemáticamente se refieren a cada una de las variables termodinámicas con relación a otra mientras todo lo demás se mantiene constante. La ley de Charles establece que el volumen y la temperatura son directamente proporcionales entre sí, siempre y cuando la presión se mantenga constante. La ley de Boyle afirma que la presión y el volumen son inversamente proporcionales entre sí a temperatura constante. Finalmente, la ley de Gay-Lussac introduce una proporcionalidad directa entre la temperatura y la presión, siempre y cuando se encuentre a un volumen constante. La interdependencia de estas variables se muestra en la ley de los gases combinados, que establece claramente que:

La relación entre el producto presión-volumen y la temperatura de un sistema permanece constante.

Matemáticamente puede formularse como:

$\qquad \frac {PV}{T}= K$

donde:

P es la presión
V es el volumen
T es la temperatura absoluta (en kelvins)
K es una constante (con unidades de energía dividido por la temperatura) que dependerá de la cantidad de gas considerado.

Otra forma de expresarlo es la siguiente:

$\qquad \frac {P_1V_1}{T_1}= \frac {P_2V_2}{T_2}$

donde presión, volumen y temperatura se han medido en dos instantes distintos 1 y 2 para un mismo sistema.

En adición de la ley de Avogadro al rendimiento de la ley de gases combinados se obtiene la ley de los gases ideales.

Ley de Boyle establece que el producto presión-volumen es constante:

(1) $PV = k_1 \qquad$

Ley de Charles muestra que el volumen es proporcional a temperatura absoluta:

(2) $V = k_2T \qquad$

Ley de Gay-Lussac dice que la presión es proporcional a la temperatura absoluta:

(3) $P = k_3T \qquad$

donde P es la presión, V el volumen y T la temperatura absoluta de un gas ideal.

Mediante la combinación de (2) o (3) podemos obtener una nueva ecuación con P, V y T.

$PV=k_{ 2 }{ k }_{ 3 }{ T }^{ 2 }$

Definiendo el producto de K₂ por K₃ como K₄:

$PV=k_{ 4 }{ T }^{ 2 }$

Multiplicando esta ecuación por (1):

${ (PV) }^{ 2 }={ k }_{ 1 }k_{ 4 }{ T }^{ 2 }$

Definiendo k₅ como el producto de k₁ por k₄ reordenando la ecuación:

$\frac { { (PV) }^{ 2 } }{ { T }^{ 2 } } ={ k }_{ 5 }$

Sacando raíz cuadrada:

$\frac { PV }{ T } ={ \sqrt { { k }_{ 5 } } }$

Renombrando la raíz cuadrada de k₅ como K nos queda la ecuación general de los gases:

$\frac { PV }{ T } = K$

LEY DE DALTON

La ley de Dalton se puede referir a 2 resultados importantes en química, formulados por John Dalton:

Ley de las presiones parciales, el cálculo de las presiones parciales de una mezcla de gases aplicando la ley de los gases ideales a cada componente.
Ley de las proporciones múltiples, utilizada en estequiometría.

LAS SOLUCIONES

- La materia se presenta con mayor frecuencia en la naturaleza en forma de soluciones, dentro de las cuales se llevan a cabo la gran mayoría de los procesos químicos.

- Muchas de estas mezclas son soluciones y todas ellas rodean a los seres vivos (agua de mar, de río, suelo, aire, sustancias comerciales, etc.), por lo que nuestra existencia depende de las mismas, en menor o mayor grado. Además, en el interior de una persona existen soluciones tales como la saliva, sangre, orina, ácidos y bases diluidos, etc.

- La industria genera infinidad de soluciones en forma de drogas, medicinas, desinfectantes, bebidas gaseosas, cosméticos, etc.

Partes de una solución (componentes)

Hay dos aspectos importantes en el tema de las soluciones: el de las partes o sustancias que las forman y el de la cantidad de cada una de estas partes, principalmente el soluto. Veremos el primer aspecto.

Toda solución está formada por dos partes: el soluto y el solvente. El soluto es la sustancia que se disuelve y que está en menor cantidad en una solución; el solvente es la sustancia que se encuentra en mayor cantidad y es la que di - suelve al soluto. La solución resulta de mezclar el soluto con el solvente, y estas sustancias mezcladas tan solo experimentan un cambio físico, específica -mente el solvente (aspecto, puntos de fusión, ebullición y congelación, etc.).

En ocasiones, existe un solvente y varios solutos, y a veces varios solventes y solutos; las partículas del soluto son moléculas o iones y se encuentran dispersas y atrapadas por las moléculas del solvente, que son más abundantes y de mayor tamaño molecular.

Con respecto al solvente, se reconoce al agua como el solvente universal o más popular; cuando el agua actúa como solvente en las soluciones, entonces estas se denominan "soluciones acuosas".Sin embargo, no todas las sustancias se disuelven en el agua, sino que lo hacen en otros tipos de solventes (alcohol, etc.), por lo que las soluciones pueden ser acuosas (cuando el agua es el solven te) y no-acuosas (cuando el solvente es otra sustancia).

Estados de las soluciones

Se sabe que toda la materia del mundo se presenta fundamentalmente en 3 estados físicos o de agregación, y en igual modo se presentan las soluciones en la naturaleza, así:

a. Soluciones sólidas. Todas las aleaciones, como el latón (cobre con zinc), bronce (cobre con es

taño), acero (carbono con hierro), etc.

b. Soluciones líquidas. Como

- Sólido en líquido: sal disuelta en agua; azúcar disuelta en agua, etc.

- Líquido en líquido: alcohol disuelto en agua, etc.

- Gas en líquido: oxígeno en agua, el gas carbónico en los refrescos, etc.

c. Soluciones gaseosas. Como el aire, que es una solución formada por varios gases (solutos), ta

les como el dióxido de carbono, oxígeno y argón, los cuales están disueltos en otro gas llama –

do nitrógeno (solvente). Otros ejemplos son la niebla y el humo.

Así, las soluciones pueden ser sólidas, liquidas y gaseosas, y estar formadas por gases (soluto) en gases (solvente), gases en líquidos, sólidos en líquidos, líquidos en líquidos y sólidos en só- lidos. Esto es que, el soluto puede ser un gas, un líquido o un sólido, e igual el solvente.

Estados de las soluciones

Estado del Solvente	Estado del Soluto	Solución que Resulta	Ejemplos
Solido	Solido	Solido	Aleaciones: bronce, latón, acero.
Liquido	Liquido	Liquida	Alcohol en agua; vino; vinagre.
Liquido	Solido	Liquida	Sal en agua; azúcar en agua.
Liquido	Gas	Liquida	Oxigeno en agua.
Gas	Gas	Gas	Aire.

Cálculo de la concentración de las soluciones

Toda persona interesada en calcular la concentración de una solución, es decir, la cantidad o proporción de soluto presente en una solución, puede auxiliarse de cualquiera de los tres méto- dos existentes para ello; en todo caso, la concentración que se calcula corresponde al de las soluciones diluidas y saturadas. He aquí los métodos.

- Método empírico o visual. Consiste en apreciar detenidamente la solución, y establecer un criterio sobre la presencia o aparente ausencia de soluto en la misma; seguidamente este criterio se compara con la definición correspondiente a cada tipo fundamental de solución(solución diluida, saturada, etc.) , y a continuación se establece definitivamente ante qué tipo de solución se está. Este método es cualitativo, y no es preciso en la determinación de la concentración de una solución, pues se basa en un criterio personal, y no en formula o calculo alguno.

Por ejemplo: si se aprecia una solución y no se observan partículas de soluto, entonces se esta ante una solución del tipo diluida o insaturada; pero si se observan algunas partículas en el fondo del recipiente que contiene a la solución en estudio, luego la solución es tipo saturada; y si en el fondo del mismo recipiente se observa una capa de soluto, entonces la solución esta sobresaturada. Por último, sí en tal recipiente existiese más soluto que solvente, definitivamente que la solución sería del tipo concentrada.

- Métodos físicos. Son sencillos, y nombrados así porque son expresiones o fórmulas que contienen unidades de medidas físicas (gramos, miligramos, etc.). Son métodos cuantitativos, y por lo tanto expresan la concentración con precisión, e indican en porcentaje (%) la cantidad de masa del soluto presente por cada cien partes de masa de la solución. Son 3 estos métodos:

Esta fórmula o expresión se utiliza cuando la masa del soluto, solvente o solución esta expresada en gramos; el peso del soluto (masa) se divide entre el peso de la solución( peso sobre peso), y este resultado parcial se multiplica por cien para obtener el resultado final, el que indica el peso del soluto por cada cien unidades de peso de de la solución.

Ejercicio 1.

¿Cuál es la concentración de la sal de mesa o cloruro de sodio (NaCl) en una solución formada por 50 gramos de agua (solvente) y 5 gramos de esta sal (soluto) ?

La sal de mesa representa al soluto y el agua al solvente; cuando ambas cantidades se suman, luego resulta la masa de la solución (agua salada).

Primer paso. Reunir los valores numéricos.

- Masa del soluto = 5 gramos.

- Masa del solvente = 45 gramos.

- Masa de la solución = 50 gramos.

Segundo paso. Aplicar la expresión o formula física de % de peso sobre peso (% p/p).

Respuesta= La concentración de la sal de cocina en la solución de agua salada es de 10%; esto significa que la solución está formada por 90 partes de solvente (agua) y 10 partes de soluto (sal de cocina), o bien, que existen 10 gramos de sal por cada 100 gramos de solución.

Ejercicio 2.

Una solución de agua azucarada pesa 120 gramos, y contiene 30 gramos de azúcar de mesa o sacarosa ( C12H22O11). ¿ Cuál es la concentración del azúcar?

El azúcar de mesa representa al soluto, la que ha sido disuelta en agua (solvente), formandose así la solución de agua azucarada.

Primer paso. Reunir los valores numéricos.

- Masa del soluto = 30 gramos.

- Masa de la solución = 120 gramos.

Segundo paso. Aplicar la expresión o formula física de % de peso sobre peso (% p/p).

Respuesta= La concentración del azúcar en la solución de agua azucarada es de 25 %; en otras palabras, el azúcar representa el 25 % de la solución.

Esta fórmula o expresión se utiliza cuando la masa del soluto esta expresada en gramos y la masa del solvente o solución están expresadas en mililitros; en otras palabras, la expresión se utiliza cuando el soluto es un sólido y el solvente o solución es un líquido. La masa del soluto se dividen entre el volumen o mililitros de la solución ( peso sobre volumen), y este resultado se multiplica por cien para obtener el resultado final, el que indica el peso en gramos del soluto que hay por cada cien mililitros de solución, o sea, en qué porcentaje está presente el soluto en comparación con toda la solución(100%).

Ejercicio 1.

¿Cuál es la concentración, o porcentaje de peso sobre volumen (%P/V) , de 30 gramos de sal de mesa en una solución de 150 mililitros de agua salada?

Observe que la masa del soluto (sal) esta expresada en gramos y que la solución(agua salada) esta expresada en unidades de volumen, o sea mililitros.

Primer paso. Reunir los valores numéricos.

- Masa del soluto (sal) = 30 gramos.

- Volumen de la solución (agua salada) = 150 ml.

Segundo paso. Aplicar la expresión o formula física de % de peso sobre volumen (% P/V).

Respuesta= La concentración de la sal de cocina en la solución de agua salada es de 20%; esto significa que por cada 100 partes de solución hay 20 partes de sal.

Ejercicio 2.

¿Cuál es la concentración, o porcentaje de peso sobre volumen (%P/V) , de 60 gramos de azúcar de mesa en una solución de 150 mililitros de agua azucarada?

El azúcar de mesa representa al soluto, la que ha sido disuelta en agua (solvente), formandose así la solución de agua azucarada.

Primer paso. Reunir los valores numéricos.

- Masa del soluto (azúcar) = 60 gramos.

- Volumen de la solución (agua azucarada) = 150 mililitros.

Segundo paso. Aplicar la expresión o formula física de % de peso sobre volumen (% p/v).

Respuesta= La concentración del azúcar en la solución de agua azucarada es de 40 %; en otras palabras, el azúcar representa el 40 % de la solución.

Esta expresión se utiliza cuando el soluto, el solvente y la solución están expresados en mililitros,o sea, en unidades de volumen; las sustancias involucradas en esta expresión deberían ser liquidas o gases. Los mililitros de soluto se dividen entre los mililitros de la solución (volumen sobre volumen), y este resultado se multiplica por cien para obtener el resultado final, el que indica el volumen de soluto presente por cada cien unidades de volumen de la solución.

Ejercicio 1.

¿Cuál es la concentración de alcohol en una solución formada por 45 mililitros de agua (solvente) y 5 ml de alcohol (soluto) ?

El alcohol representa al soluto, el que ha sido disuelto en agua (solvente), formándose así la solución de agua alcoholizada.

Primer paso. Reunir los valores numéricos.

- Volumen del soluto = 5 ml de alcohol

- Volumen del solvente = 45 ml de agua

- Volumen de la solución = 50 ml de agua alcoholizada.

Segundo paso. Aplicar la expresión física de % de volumen sobre volumen (% V/V).

Respuesta= La concentración del alcohol en la solución es de 10 % , esto es, que por cada 100 partes de solución existen 10 partes de alcohol.

Ejercicio 2.

Una solución está formada por 400 ml de Ácido Clorhídrico (HCI) y 1,600 ml de agua ¿Cual es la concentración del ácido en % de volumen sobre volumen ?

El HCl representa al soluto, el que ha sido disuelto en agua (solvente), formándose así la solución de agua y acido.

Primer paso. Reunir los valores numéricos.

- Volumen del soluto = 400 ml

- Volumen del solvente = 1,600 ml

- Volumen de la solución = 2,000 ml

Segundo paso. Aplicar la expresión física de % de volumen sobre volumen (% v/v).

Respuesta= La concentración del ácido en la solución es de 20 % , o sea, que por cada 100 partes de solución existen 20 partes de ácido.

Existe otro método físico denominado "partes por millón", que se utiliza para calcular la concentración de aquellas soluciones que contienen cantidades muy ínfimas (pequeñísimas) de soluto, como por ejemplo menos de un gramo. Su planteamiento es:

- Métodos químicos. Son menos sencillos, cuyas formulas o expresiones contienen unidades de medida químicas(moles, equivalentes, etc.) y físicas. Son cuantitativos y precisos. He aquí tres de ellos :

Esta expresión se utiliza cuando la solución es líquida y que se puede medir con un simple equipo volumétrico, como probeta, bureta, etc.

En la formula se utiliza una unidad de medida química (mol) y otra física (litro); ello significa que, la masa del soluto se expresa en moles y la de la solución en litros. La cantidad de soluto se divide entre la de la solución, y el valor obtenido representa la molaridad (M) de la solución, que se interpreta como la cantidad de moles del soluto presentes en 1 litro de solución.

Una solución uno molar (1 M) significa que un mol de soluto esta disuelto en un litro de solucion. Un mol se refiere a una cierta cantidad de átomos o moléculas de cualquier sustancia, y esa cantidad equivale a seis mil trillones de átomos o moléculas, esto es 6 x 1023 , lo que se conoce como numero de Avogadro. Entonces, un mol de agua está formado por seis mil trillones de moléculas de H2O

Ejercicio 1.

Una solución de 2 litros contiene 0.5 moles de KCl ¿ Cuál es la molaridad de la solución ?

Primer paso. Reunir los valores numéricos.

- Cantidad de soluto = 0.5 moles de KCl

- Cantidad de la solución = 2 litros

Segundo paso. Aplicar la expresión química de molaridad.

En los 2 litros de solución tan solo están diluidos un cuarto de mol de KCl; en otras palabras, existen un mil quinientos trillones de moléculas de KCl diluidas en los 2 litros de solución.

En ciertos ejercicios la cantidad del soluto no está dada en moles, sino que estará expresada en gramos, por lo que habrá que convertir estos gramos a moles, antes de utilizar la expresión o formula de Molaridad. Por ejemplo:

Ejercicio 2.

Una solución de 2 litros contiene 148 gramos de KCl ¿ Cuál es la molaridad de la solución ?

Primer paso. Reunir los valores numéricos.

- Cantidad de soluto = 148 gramos de KCl

- Cantidad de la solución = 2 litros

Segundo paso. Convertir los gramos de soluto a moles.

- Primero se obtiene el peso molecular del soluto (ver tabla periódica), en gramos, así:

- Estos 74 gramos de KCl equivalen a 1 mol. A continuación se plantea una regla de tres:

Los 148 gramos de KCl equivalen a 2 moles de la misma sustancia.

Tercer paso. Aplicar la expresión química de molaridad.

En los dos litros de solución están diluidos 2 moles de KCl; expresado de otro modo, existen doce mil trillones de moléculas de KCl diluidas en los 2 litros de solución (seis mil trillones por cada mol).

Este planteamiento se utiliza en los casos en que se conoce la cantidad de soluto y de solvente, pero la solución aún no está hecha como para medirla y, sin embargo, desea conocerse la concentración de la futura solución. También hay ocasiones en que es más conveniente medir el soluto en lugar del volumen de la solución.

Esta expresión o formula utiliza una unidad de medida química (mol) y otra física (kg); esto significa que, la masa del soluto se expresa en moles y la del solvente en kg. La cantidad de soluto se divide entre la cantidad del solvente, y el valor obtenido representa a la molalidad (m) de la solución, que se interpreta como la cantidad de moles de soluto disueltos por un kilogramo de solvente.

Una solución uno molal (1 m) significa que un mol de soluto esta disuelto por un kilogramo

de solvente, o que la solución está formada por un mol de soluto y un kilogramo de solvente.

Ejercicio 1.

Una solución de agua azucarada contiene 2 moles de azúcar (C12H22O11) y 4 kilogramo de agua ¿ Cuál es la molalidad de la solución ?

Primer paso. Reunir los valores numéricos.

- Cantidad de soluto = 2 moles de azúcar de mesa.

- Cantidad de solvente = 4 kilogramos de agua.

Segundo paso. Aplicar la expresión química de Molalidad.

La concentración de azúcar es de medio mol por cada kilogramo de agua, que equivale a decir, que en cada kilogramo de agua esta disuelto medio mol de azúcar (unas tres mil trillones de moléculas).

En ciertos ejercicios la cantidad del soluto no está dada en moles, sino que estará expresada en gramos, al igual que el solvente, por lo que habrá que convertir estos a moles y kilogramos,

respectivamente, antes de utilizar la expresión o formula de molalidad. Por ejemplo:

Ejercicio 2.

Una solución de agua azucarada contiene 57 gramos de azúcar (C12H22O11) y 250 gramos de agua ¿ Cuál es la molalidad de la solución ?

Primer paso. Reunir los valores numéricos.

- Cantidad de soluto = 171 gramos de azúcar.

- Cantidad de solvente = 250 gramos de agua.

Segundo paso. Convertir los gramos de soluto y solvente a moles y kilogramos, respectivamente.

- Primero se obtiene el peso molecular del soluto (ver tabla periódica), en gramos, así:

- Estos 342 gramos de azúcar equivalen a 1 mol. A continuación se plantea una regla de tres, así:

Los 342 gramos de azúcar equivalen a 0.5 moles de la misma sustancia.

Tercer paso. Convertir los gramos de solvente (agua) a kilogramos:

Cuarto paso. Aplicar la expresión química de molalidad.

La concentración de azúcar en la solución es de 2 moles por cada kilogramo de agua, que equivale a decir, que en cada kilogramo de agua están disueltos dos moles de azúcar(unas doce mil trillones de moléculas).

Ejercicio 3.

Se preparo una solución con 15 gramos de Cloruro de Sodio(sal de mesa) y 2 litros de agua.

¿ Cuál es la molalidad de la solución ?

Primer paso. Reunir los valores numéricos.

- Cantidad de soluto = 15 gramos de sal (NaCl).

- Cantidad de solvente = 2 litros de agua.

Segundo paso. Convertir los gramos de soluto a moles, y los litros de solvente a kilogramos.

- Primero se obtiene el peso molecular del soluto (ver tabla periódica), en gramos, así:

- Estos 58 gramos de sal equivalen a 1 mol. A continuación se plantea una regla de tres, así:

Los 15 gramos de sal equivalen a 0.25 moles de la misma sustancia.

Tercer paso. Convertir los 2 litros de solvente (agua) a kilogramos: un litro de agua equivale a un kilogramo de la misma sustancia, entonces

Cuarto paso. Aplicar la expresión química de molalidad.

La concentración de azúcar en la solución es de 0.125 moles por cada kilogramo de agua.

Esta expresión se utiliza en aquellos casos en que la solución será empleada en reacciones de ácidos con bases.

Se interpreta como la cantidad de equivalentes gramos de soluto contenidos en un litro de solución. En la expresión anterior, equivalentes gramos de soluto se refiere a peso equivalente gramo del soluto, lo que se define de tres maneras, según sea el tipo de sustancia:

Para determinar la normalidad de una solución, habrá que calcular primeramente el peso equivalente-gramo del soluto de que se trate (elemento, acido o base), y este resultado, junto con el de litros de solución, se introducen en la expresión o formula de Normalidad.

Ejercicio 1.

¿Cuál es la normalidad de una solución de 1 litro que contiene 4 gramos de HCl o acido clorhídrico?

Primer paso. Reunir los valores numéricos.

- Cantidad de sustancia acida o soluto = 18 gramos.

- Cantidad de solución = 1 litro.

Segundo paso. Calcular el peso equivalente-gramo de la sustancia acida.

- Calcular el peso o masa molecular del soluto (HCl).